Stochastic Schrödinger Equations and Conditional States: A General Non-Markovian Quantum Electron Transport Simulator for THz Electronics
Abstract
:1. Introduction
2. Electron Devices as Open Quantum Systems
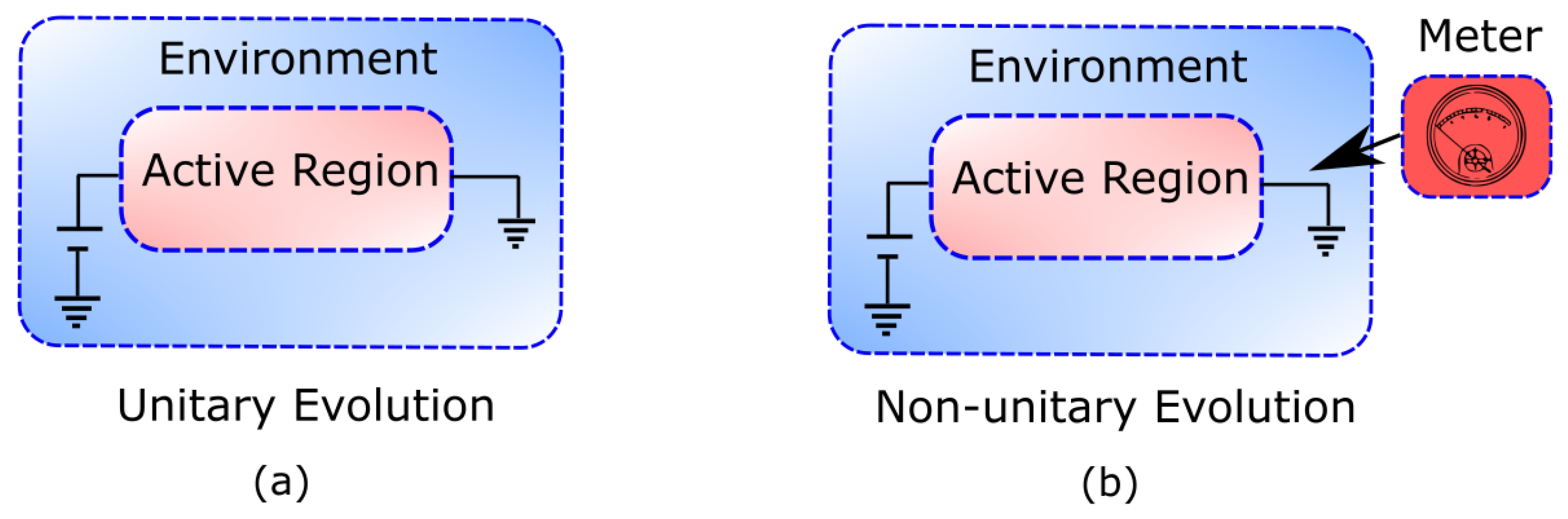
2.1. Open Quantum Systems
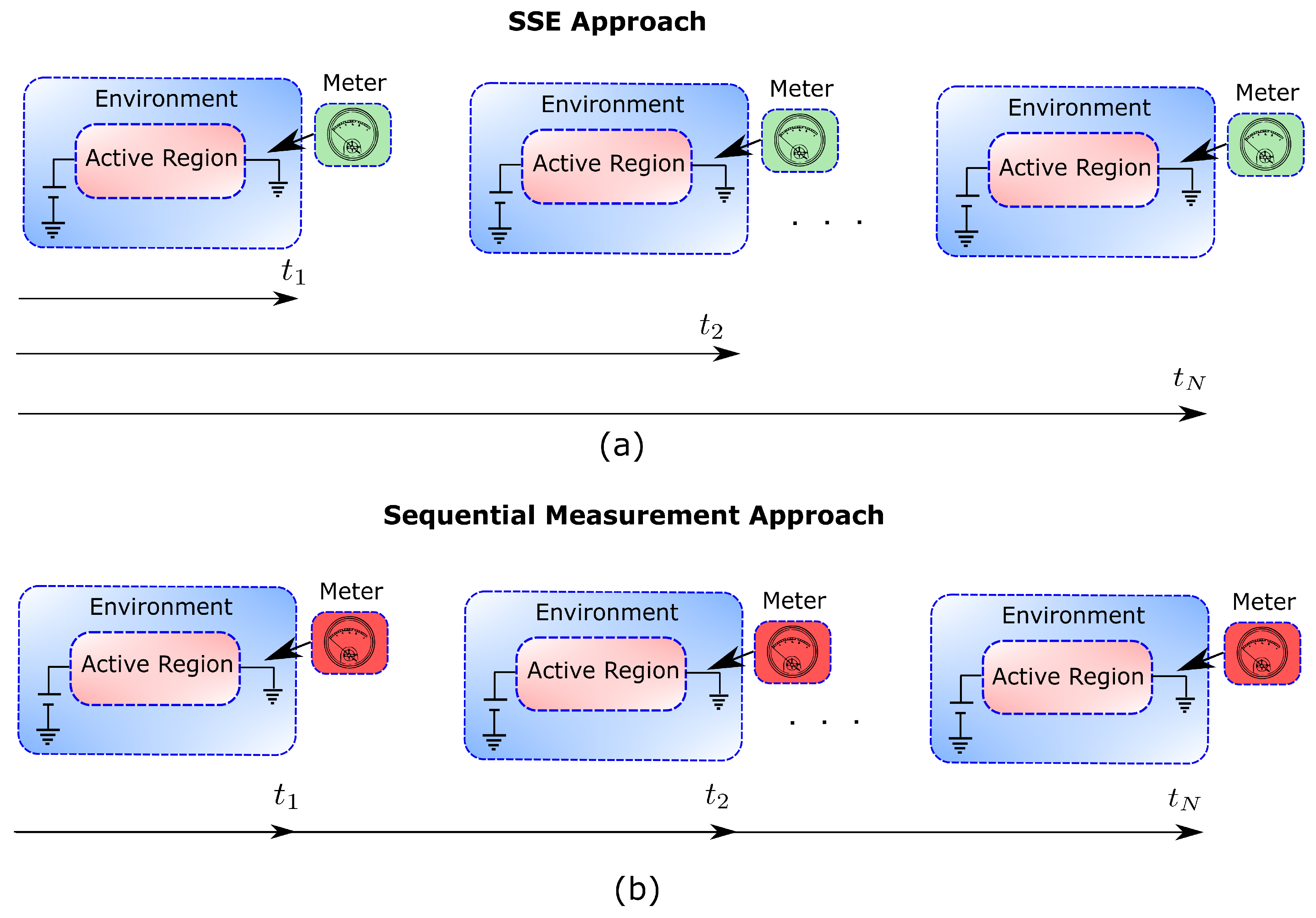
2.2. Stochastic Schrodinger Equations
2.3. Nanoscale Electron Devices as Open Quantum Systems
3. Interpretation of Conditional States in Open Quantum Systems
3.1. The Orthodox Interpretation of Conditional States
3.1.1. Orthodox Conditional States in Markovian Scenarios
3.1.2. Orthodox Conditional States in Non-Markovian Scenarios
3.2. The Bohmian Interpretation of Conditional States
4. Bohmian Conditional Wavefunction Approach to Quantum Electron Transport
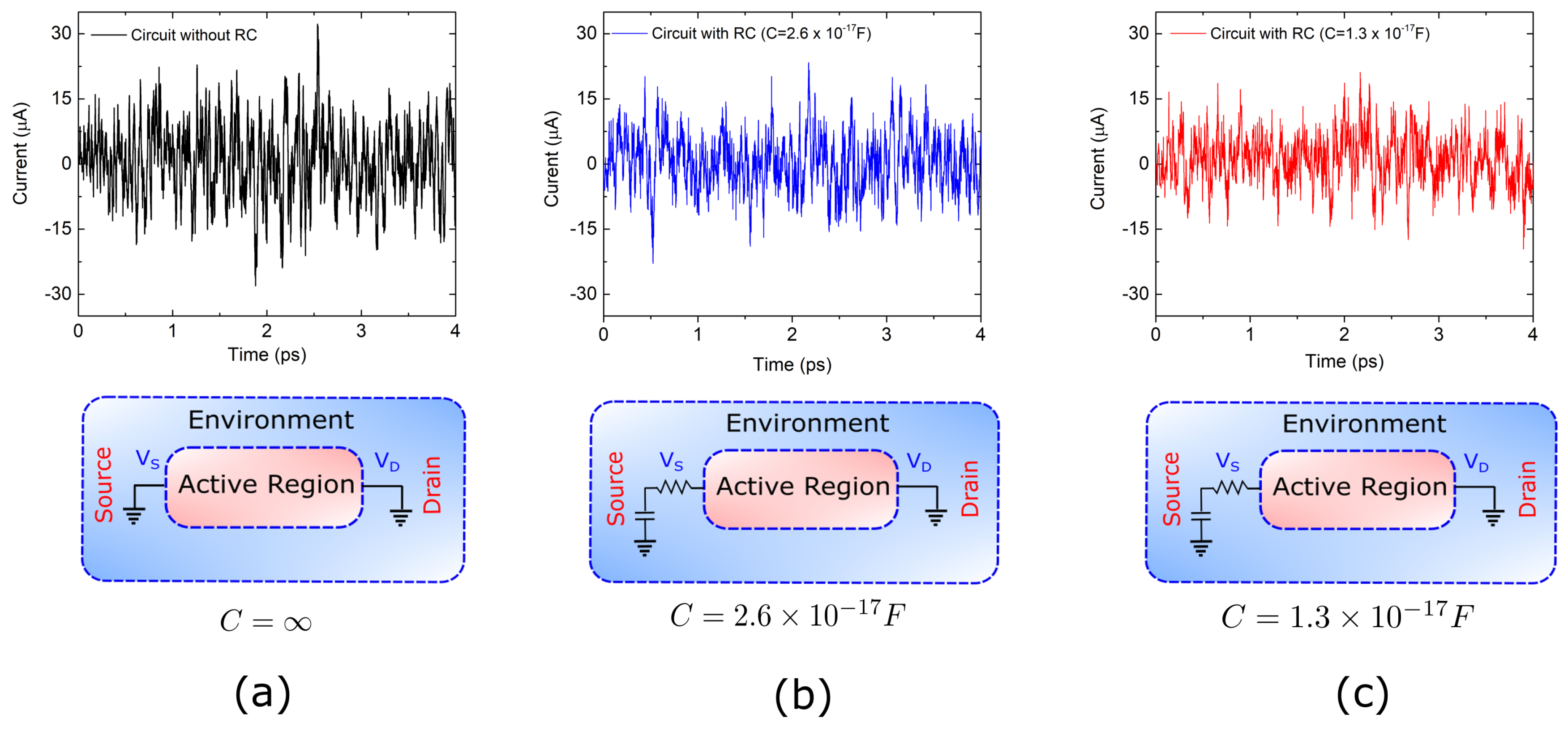
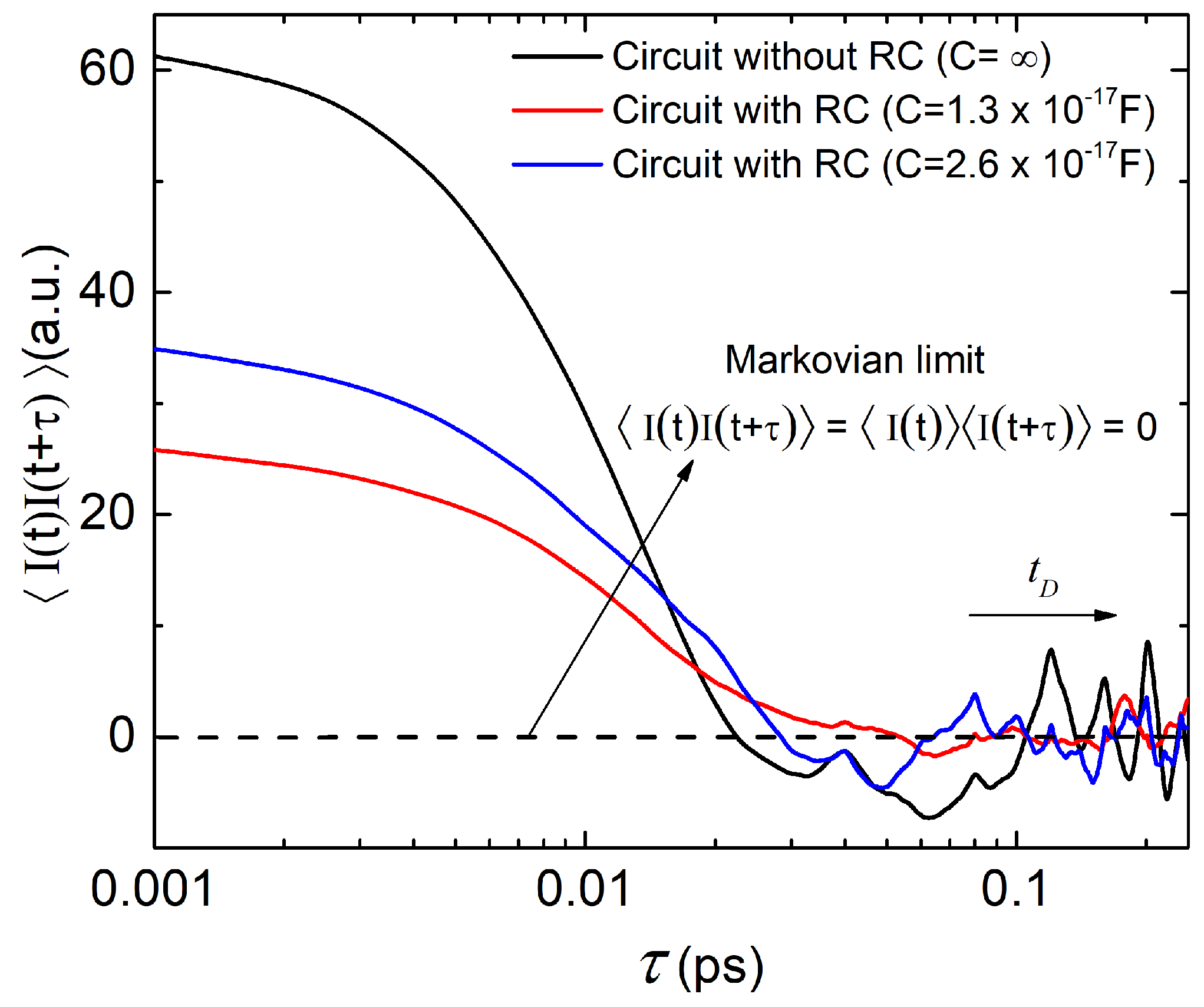
5. Numerical Results
6. Conclusions and Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. D’Espagnat Distinction between “Proper” and “Improper” Mixtures
- The “proper” mixture is simply a mixture of different pure states of a closed system. We define such pure states as with . We know that each of these states represent the closed system in one of the repeated experiments, but we ignore which state corresponds to each experiment. We only know the probability that one experiment is represented by the pure state . Then, if we are interested in computing some ensemble value of the system, over all experiments, von Neumann introduced the mixture . It is important to notice that we are discussing here human ignorance (not quantum uncertainty). The system is always in a well-defined state (for all physical computations), but we (the humans) ignore what the state is in each experiment.
- The “improper” mixture refers to the density matrix that results from a trace reduction of a pure sate (or statistical operator) of a whole system that includes the system and the environment. The reduced density of the system alone is given by tracing out the degrees of freedom of the environment, giving the result in Equation (7), which is mathematically (but not physically) equivalent to the results of the "proper" mixture constructed from our “ignorance” of which state represents the system.
Appendix B. Orthodox and Bohmian Reduced Density Matrices
Appendix C. Equations of Motion for Single-Electron Conditional States in Graphene
References
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645. [Google Scholar] [CrossRef]
- Available online: http://www.nextnano.de (accessed on 22 November 2019).
- Available online: http://www.tibercad.org (accessed on 22 November 2019).
- Available online: http://vides.nanotcad.com/vides/ (accessed on 22 November 2019).
- Albareda, G.; Jiménez, D.; Oriols, X. Intrinsic noise in aggressively scaled field-effect transistors. J. Stat. Mech. Theory Exp. 2009, 2009, P01044. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Smirne, A.; Breuer, H.P.; Piilo, J.; Vacchini, B. Initial correlations in open-systems dynamics: The Jaynes-Cummings model. Phys. Rev. A 2010, 82, 062114. [Google Scholar] [CrossRef]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Vacchini, B. Non-Markovian dynamics for bipartite systems. Phys. Rev. A 2008, 78, 022112. [Google Scholar] [CrossRef]
- Gisin, N. Stochastic quantum dynamics and relativity. Helv. Phys. Acta 1989, 62, 363–371. [Google Scholar]
- Pearle, P. Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 1989, 39, 2277. [Google Scholar] [CrossRef]
- Carmichael, H. An Open Systems Approach to Quantum Optics: Lectures Presented at the Université Libre de Bruxelles, October 28 to November 4 1991; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 18. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Radarweg/Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- De Vega, I. Non-Markovian stochastic Schrödinger description of transport in quantum networks. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 245501. [Google Scholar] [CrossRef]
- Goetsch, P.; Graham, R. Linear stochastic wave equations for continuously measured quantum systems. Phys. Rev. A 1994, 50, 5242. [Google Scholar] [CrossRef]
- Gatarek, D.; Gisin, N. Continuous quantum jumps and infinite-dimensional stochastic equations. J. Math. Phys. 1991, 32, 2152–2157. [Google Scholar] [CrossRef]
- Gambetta, J.; Wiseman, H. Non-Markovian stochastic Schrödinger equations: Generalization to real-valued noise using quantum-measurement theory. Phys. Rev. A 2002, 66, 012108. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Diósi, L. Non-Markovian continuous quantum measurement of retarded observables. Phys. Rev. Lett. 2008, 100, 080401. [Google Scholar] [CrossRef] [PubMed]
- Wiseman, H.M.; Gambetta, J.M. Pure-state quantum trajectories for general non-Markovian systems do not exist. Phys. Rev. Lett. 2008, 101, 140401. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, B.; Oriols, X.; Ferry, D. Dynamics of current, charge and mass. Comput. Math. Biophys. 2017, 5, 78–115. [Google Scholar] [CrossRef]
- Oriols, X.; Ferry, D. Quantum transport beyond DC. J. Comput. Electron. 2013, 12, 317–330. [Google Scholar] [CrossRef]
- Gambetta, J.; Wiseman, H. Interpretation of non-Markovian stochastic Schrödinger equations as a hidden-variable theory. Phys. Rev. A 2003, 68, 062104. [Google Scholar] [CrossRef]
- Gambetta, J.; Wiseman, H. Modal dynamics for non-orthogonal decompositions. Found. Phys. 2003, 34, 419–448. [Google Scholar] [CrossRef]
- Colomés, E.; Zhan, Z.; Marian, D.; Oriols, X. Quantum dissipation with conditional wave functions: Application to the realistic simulation of nanoscale electron devices. Phys. Rev. B 2017, 96, 075135. [Google Scholar] [CrossRef]
- Oriols, X. Quantum-Trajectory Approach to Time-Dependent Transport in Mesoscopic Systems with Electron-Electron Interactions. Phys. Rev. Lett. 2007, 98, 066803. [Google Scholar] [CrossRef]
- Alarcón, A.; Yaro, S.; Cartoixa, X.; Oriols, X. Computation of many-particle quantum trajectories with exchange interaction: Application to the simulation of nanoelectronic devices. J. Phys. Condens. Matter 2013, 25, 325601. [Google Scholar] [CrossRef] [PubMed]
- Albareda, G.; López, H.; Cartoixa, X.; Suné, J.; Oriols, X. Time-dependent boundary conditions with lead-sample Coulomb correlations: Application to classical and quantum nanoscale electron device simulators. Phys. Rev. B 2010, 82, 085301. [Google Scholar] [CrossRef]
- Albareda, G.; Suñé, J.; Oriols, X. Many-particle hamiltonian for open systems with full coulomb interaction: Application to classical and quantum time-dependent simulations of nanoscale electron devices. Phys. Rev. B 2009, 79, 075315. [Google Scholar] [CrossRef]
- Nakajima, S. On quantum theory of transport phenomena: Steady diffusion. Prog. Theor. Phys. 1958, 20, 948–959. [Google Scholar] [CrossRef]
- Zwanzig, R. Ensemble method in the theory of irreversibility. J. Chem. Phys. 1960, 33, 1338–1341. [Google Scholar] [CrossRef]
- Dalibard, J.; Castin, Y.; Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 1992, 68, 580. [Google Scholar] [CrossRef]
- Strunz, W.T.; Diósi, L.; Gisin, N. Open system dynamics with non-Markovian quantum trajectories. Phys. Rev. Lett. 1999, 82, 1801. [Google Scholar] [CrossRef]
- Barchielli, A.; Gregoratti, M. Quantum measurements in continuous time, non-Markovian evolutions and feedback. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 5364–5385. [Google Scholar] [CrossRef]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kraus, K. States, Effects and Operations: Fundamental Notions of Quantum Theory; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum state diffusion. Phys. Rev. A 1998, 58, 1699. [Google Scholar] [CrossRef]
- Gambetta, J.; Wiseman, H. Perturbative approach to non-Markovian stochastic Schrödinger equations. Phys. Rev. A 2002, 66, 052105. [Google Scholar] [CrossRef]
- Budini, A.A. Non-Markovian Gaussian dissipative stochastic wave vector. Phys. Rev. A 2000, 63, 012106. [Google Scholar] [CrossRef]
- Bassi, A.; Ghirardi, G. Dynamical reduction models with general Gaussian noises. Phys. Rev. A 2002, 65, 042114. [Google Scholar] [CrossRef] [Green Version]
- Bassi, A. Stochastic Schrödinger equations with general complex Gaussian noises. Phys. Rev. A 2003, 67, 062101. [Google Scholar] [CrossRef] [Green Version]
- D’Espagnat, B. Conceptual Foundations of Quantum Mechanics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Benseny, A.; Albareda, G.; Sanz, Á.S.; Mompart, J.; Oriols, X. Applied bohmian mechanics. Eur. Phys. J. D 2014, 68, 286. [Google Scholar] [CrossRef] [Green Version]
- Pladevall, X.O.; Mompart, J. Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Holland, P.R. The Quantum Theory of Motion: An Account of the De Broglie-Bohm Causal Interpretation of Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 1952, 85, 166. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Tumulka, R.; Zanghi, N. Bohmian mechanics and quantum field theory. Phys. Rev. Lett. 2004, 93, 090402. [Google Scholar] [CrossRef] [Green Version]
- Dürr, D.; Goldstein, S.; Zanghi, N. Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 1992, 67, 843–907. [Google Scholar] [CrossRef] [Green Version]
- Pandey, D.; Sampaio, R.; Ala-Nissila, T.; Albareda, G.; Oriols, X. Unmeasured Bohmian properties and their measurement through local-in-position weak values for assessing non-contextual quantum dynamics. 2019; submitted. [Google Scholar]
- Alarcón, A.; Albareda, G.; Traversa, F.L.; Benali, A.; Oriols, X. Nanoelectronics: Quantum electron transport. In Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology; Pan Standford Publishing: Singapore, 2012; pp. 365–424. [Google Scholar]
- Albareda, G.; Marian, D.; Benali, A.; Yaro, S.; Zanghì, N.; Oriols, X. Time-resolved electron transport with quantum trajectories. J. Comput. Electron. 2013, 12, 405–419. [Google Scholar] [CrossRef]
- Albareda, G.; Marian, D.; Benali, A.; Alarcón, A.; Moises, S.; Oriols, X. Electron Devices Simulation with Bohmian Trajectories. In Simulation of Transport in Nanodevices; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 7; pp. 261–318. [Google Scholar] [CrossRef]
- Marian, D.; Colomés, E.; Oriols, X. Time-dependent exchange and tunneling: Detection at the same place of two electrons emitted simultaneously from different sources. J. Phys. Condens. Matter 2015, 27, 245302. [Google Scholar] [CrossRef] [Green Version]
- Marian, D.; Colomés, E.; Zhan, Z.; Oriols, X. Quantum noise from a Bohmian perspective: Fundamental understanding and practical computation in electron devices. J. Comput. Electron. 2015, 14, 114–128. [Google Scholar] [CrossRef] [Green Version]
- Alarcón, A.; Oriols, X. Computation of quantum electron transport with local current conservation using quantum trajectories. J. Stat. Mech. Theory Exp. 2009, 2009, P01051. [Google Scholar] [CrossRef]
- López, H.; Albareda, G.; Cartoixà, X.; Suñé, J.; Oriols, X. Boundary conditions with Pauli exclusion and charge neutrality: application to the Monte Carlo simulation of ballistic nanoscale devices. J. Comput. Electron. 2008, 7, 213–216. [Google Scholar] [CrossRef]
- Albareda, G.; Appel, H.; Franco, I.; Abedi, A.; Rubio, A. Correlated electron-nuclear dynamics with conditional wave functions. Phys. Rev. Lett. 2014, 113, 083003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norsen, T.; Marian, D.; Oriols, X. Can the wave function in configuration space be replaced by single-particle wave functions in physical space? Synthese 2015, 192, 3125–3151. [Google Scholar] [CrossRef] [Green Version]
- Albareda, G.; Kelly, A.; Rubio, A. Nonadiabatic quantum dynamics without potential energy surfaces. Phys. Rev. Mater. 2019, 3, 023803. [Google Scholar] [CrossRef] [Green Version]
- Zhan, Z.; Kuang, X.; Colomés, E.; Pandey, D.; Yuan, S.; Oriols, X. Time-dependent quantum Monte Carlo simulation of electron devices with two-dimensional Dirac materials: A genuine terahertz signature for graphene. Phys. Rev. B 2019, 99, 155412. [Google Scholar] [CrossRef] [Green Version]
- Albareda, G.; Benali, A.; Oriols, X. Self-consistent time-dependent boundary conditions for static and dynamic simulations of small electron devices. J. Comput. Electron. 2013, 12, 730–742. [Google Scholar] [CrossRef]
- Marian, D.; Zanghì, N.; Oriols, X. Weak values from displacement currents in multiterminal electron devices. Phys. Rev. Lett. 2016, 116, 110404. [Google Scholar] [CrossRef] [Green Version]
- Albareda, G.; Traversa, F.; Benali, A.; Oriols, X. Computation of quantum electrical currents through the Ramo–Shockley–Pellegrini theorem with trajectories. Fluct. Noise Lett. 2012, 11, 1242008. [Google Scholar] [CrossRef]
- Pandey, D.; Bellentani, L.; Villani, M.; Albareda, G.; Bordone, P.; Bertoni, A.; Oriols, X. A Proposal for Evading the Measurement Uncertainty in Classical and Quantum Computing: Application to a Resonant Tunneling Diode and a Mach-Zehnder Interferometer. Appl. Sci. 2019, 9, 2300. [Google Scholar] [CrossRef] [Green Version]
- Misra, B.; Sudarshan, E.G. The Zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef] [Green Version]
- Home, D.; Whitaker, M. A conceptual analysis of quantum Zeno; paradox, measurement, and experiment. Ann. Phys. 1997, 258, 237–285. [Google Scholar] [CrossRef] [Green Version]
- Colodny, R.G. Paradigms and Paradoxes: The Philosophical Challenge of The Quantum Domain; University of Pittsburgh Press: London, UK, 1972; Volume 5. [Google Scholar]
- Cabello, A.; Gu, M.; Gühne, O.; Larsson, J.Å.; Wiesner, K. Thermodynamical cost of some interpretations of quantum theory. Phys. Rev. A 2016, 94, 052127. [Google Scholar] [CrossRef] [Green Version]



| Computational Element | N° of Trajectories | N° of Degrees of Freedom | Computational Cost | ||
|---|---|---|---|---|---|
| (a) | Full wave function | – | |||
| (b) | Density Matrix | – | |||
| (c) | Orthodox Conditional state (SSE) | M | |||
| (d) | Bohmian Conditonal state | M | |||
| (e) | Bohmian Conditonal state (used in Section 5) | M | |||
| Validity of Conditional States to Provide Dynamic Information | Non-Markovian -Measured- | Non-Markovian -Unmeasured- | Non-Markovian -(Un)measured- | Markovian -(Un)measured- |
|---|---|---|---|---|
| Orthodox | (O1) ✓ | (O2) ✗ | (O3) ✗ | (O4) ✓ |
| Bohmian | (B1) ✓ | (B2) ✓ | (B3) ✓ | (B4) ✓ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, D.; Colomés, E.; Albareda, G.; Oriols, X. Stochastic Schrödinger Equations and Conditional States: A General Non-Markovian Quantum Electron Transport Simulator for THz Electronics. Entropy 2019, 21, 1148. https://doi.org/10.3390/e21121148
Pandey D, Colomés E, Albareda G, Oriols X. Stochastic Schrödinger Equations and Conditional States: A General Non-Markovian Quantum Electron Transport Simulator for THz Electronics. Entropy. 2019; 21(12):1148. https://doi.org/10.3390/e21121148
Chicago/Turabian StylePandey, Devashish, Enrique Colomés, Guillermo Albareda, and Xavier Oriols. 2019. "Stochastic Schrödinger Equations and Conditional States: A General Non-Markovian Quantum Electron Transport Simulator for THz Electronics" Entropy 21, no. 12: 1148. https://doi.org/10.3390/e21121148





